Има случаи, когато в извадката може да попаднат стойности, които значително се различават от останалите. Те се наричат отличителни или екстремни и могат да бъдат необичайно високи или ниски.
Присъствието на отличителни стойности в извадката може да се отрази негативно върху работата на моделите за машинно обучение и затова е необходимо те да се обработват по подходящ начин. В противен случай, получените резултати от модела за машинно обучение могат да бъдат доста подвеждащи.
Върху кои алгоритми оказват влияние?
- линейни модели (например регресионни и дискриминантен анализ)
- SVM
- Adaboost
Много алгоритми са чувствителни, ако при входните данни има екстремни стойности. Някои от тях очакват променливите да имат точно определено разпределение и стойностите да са в съответен интервал. Ако тези критерии не са изпълнени, тогава точността на получените резултати от моделите може да не е толкова висока.
В тази статия ще ви покажа някои основни методи за откриване на отличителни стойности в извадката, както и по какви начини могат те да бъдат обработени чрез Python.
За примерите, които ще видите по-надолу в статията, е използвана една малка извадка, съдържаща 163 записа, с данни за възрастта и годишния доход на клиенти. Можете да я изтеглите от тук.
Първите 5 реда изглеждат по следния начин:
| Age | YearlyIncome | |
|---|---|---|
| 0 | 50 | 90000 |
| 1 | 51 | 60000 |
| 2 | 51 | 60000 |
| 3 | 49 | 70000 |
| 4 | 48 | 80000 |
Как да открием отличителни стойности? Основни методи
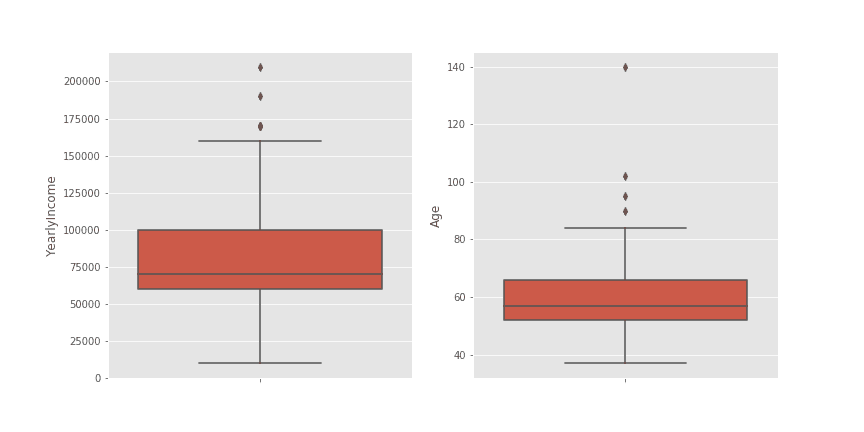
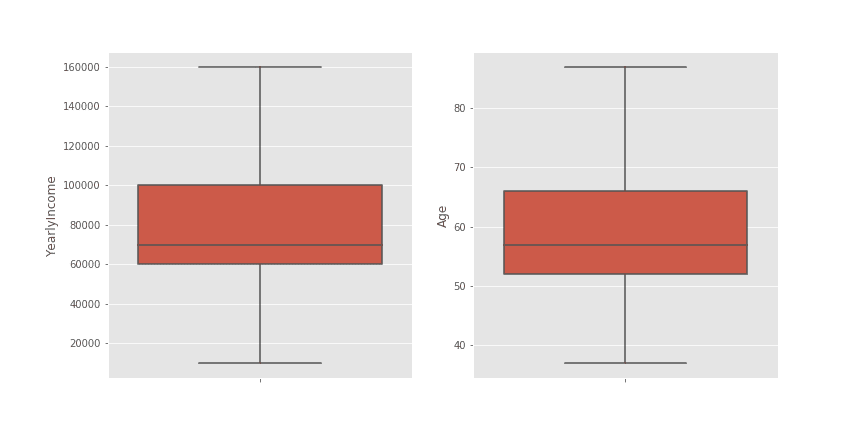
- Диаграма тип кутия (Box plot)
Отличителните стойности са всички, които са извън следните граници:
- Lower Limit = Q1 + IQR * 1.5
- Upper Limit = Q3 + IQR * 1.5
Възможно е също интерквартилният размах да се умножи по 3 вместо 1.5, за откриване на още по-високи и по-ниски стойности.
На изображението се забелязва, че извадката съдържа стойности, които са необичайно високи. При YearlyIncome това са стойности, които са над 160 000, а при Age са над 83. Медианата на годишния доход е 70000, а на възрастта е 57.
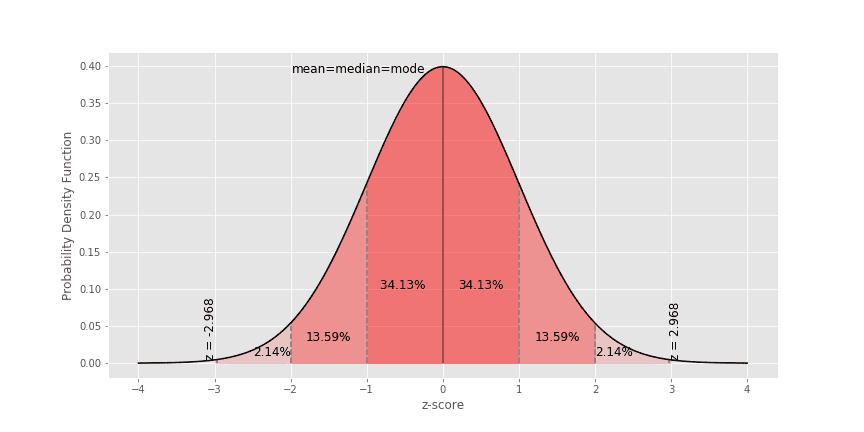
- Z-score
Z-score представлява число, което показва колко се отдалечава дадена точка от средната, измерено в стандартни отклонения.
При нормално разпределение, в интервала от -3 до 3 стандартни отклонения попадат 99.7% от данните. Всичко, което е извън този интервал, може да се определи като отличителна стойност, т.е. това e всяка стойност, която е по-ниска или по-висока от средната +– 3 пъти стандартното отклонение.
Разбира се методите не се изчерпват до тук, тъй като анализът и откриването на отличителни стойности е много обширна област. Освен тези два метода могат да се използват например и линейни модели (линейна регресия, метод на главните компоненти и др.). Също така диаграмите тип кутия не са единствените визуализации, които дават информация дали има отличителни стойности в извадката. За тази цел можем да използваме и хистограми, диаграми на разсейването и Q-Q графики например.
Кои са начините да се справим с тях?
Премахване на редове
Макар че този метод е доста бърз, предприемането му си има своите рискове. Отличителните стойности е възможно да съдържат важна информация или ако те са много, това може да доведе до премахване на голяма част от извадката.
#Взимане на индексите на редовете, които трябва да се премахнат
indexes = df[ (df['YearlyIncome'] > 160000) | (df['Age'] > 83) ].index
#Премахване на редовете
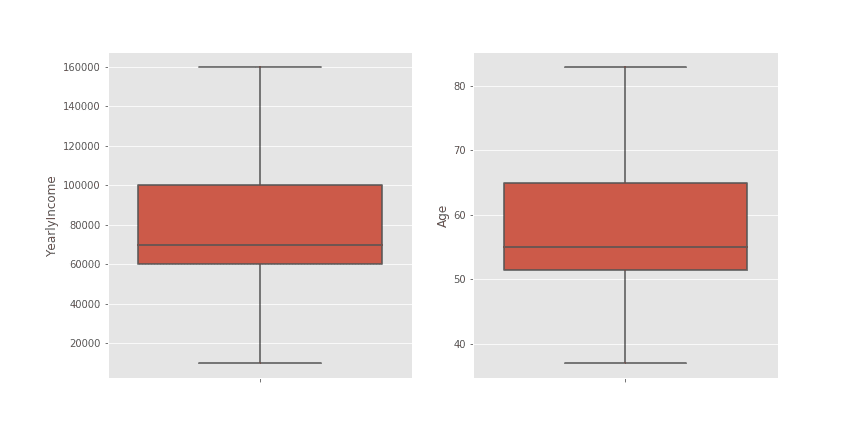
df.drop(indexes, inplace=True)Диаграмите тип кутия след премахване на отличителните стойности изглеждат по следния начин:
От визуализацията става ясно, че медианата на характеристиката YearlyIncome е 70000, а на Age е 55, т.е. премахването на редовете е довело до незначителна разлика в медианата на променливата Age.
Третиране като липсващи стойности
Отличителните стойности могат да бъдат възприети като липсващи стойности и да бъдат обработени като такива. В нашия случай ще ги заместим с медианите на съответните променливи.
#Откриване на медианите
median_income = df.loc[df['YearlyIncome'] > 160000, 'YearlyIncome'].median()
median_age = df.loc[df['Age'] > 83, 'Age'].median()
#Превръщане на отличителните стойности в NaN
df.loc[(df['YearlyIncome'] > 160000) | (df['Age'] > 83)]=np.nan
#Заместване на отличителните стойности с медиана
df['YearlyIncome'].fillna(value = median_income, inplace=True)
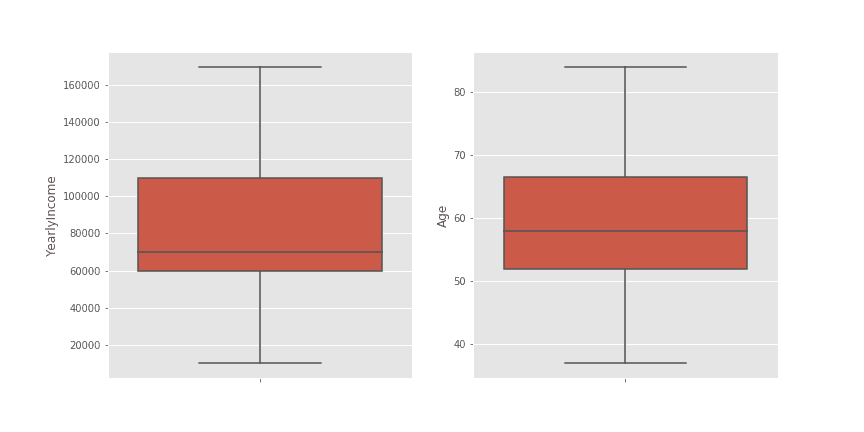
df['Age'].fillna(value = median_age, inplace=True)Диаграмите тип кутия след заместване на отличителните стойности с медиана изглеждат по следния начин:
При този пример медианата на YearlyIncome отново остава непроменена – 70000, а на Age е 58. Отново обработката на отличителните стойности е довела до незначителна разлика в медианата на променливата Age.
Ако искате да научите за други методи, чрез които да обработвате липсващи стойности, можете да прочетете в статията Machine Learning: Как да обработим липсващи стойности при подготовката на данни за анализ?
Дискретизация
Дискретизацията е процес на трансформация на непрекъснати променливи в дискретни, като стойностите се разпределят в определен брой интервали (bins).
#Изчисляване на размаха на променливите
age_range = df['Age'].max() - df['Age'].min()
income_range = df['YearlyIncome'].max() - df['YearlyIncome'].min()
# Изчисляване на долна и горна граница
min_value_age = int(np.floor( df['Age'].min()))
max_value_age = int(np.ceil( df['Age'].max()))
min_value_income = int(np.floor( df['YearlyIncome'].min()))
max_value_income = int(np.ceil( df['YearlyIncome'].max()))
# Намиране ширината на интервалите
inter_value_age = int(np.round(age_range / 5))
inter_value_income = int(np.round(income_range / 5))
# Създаване на интервалите
intervals_age = [i for i in range(min_value_age, max_value_age+inter_value_age, inter_value_age)]
intervals_income = [i for i in range(min_value_income, max_value_income+inter_value_income, inter_value_income)]
# Номериране на интервалите
labels_age = ['Bin_' + str(i) for i in range(1, len(intervals_age))]
labels_income = ['Bin_' + str(i) for i in range(1, len(intervals_income))]
# Създаване на новите колони с дискретизираните данни
df['Age_disc_labels'] = pd.cut(x=df['Age'],
bins=intervals_age,
labels=labels,
include_lowest=True)
df['Age_disc'] = pd.cut(x=df['Age'],
bins=intervals_age,
include_lowest=True)
df['YearlyIncome_disc_labels'] = pd.cut(x=df['YearlyIncome'],
bins=intervals_income,
labels=labels,
include_lowest=True)
df['YearlyIncome_disc'] = pd.cut(x=df['YearlyIncome'],
bins=intervals_income,
include_lowest=True)
# Преглет на данните
df.sample(frac=1).head(10)Резултат:
| Age | YearlyIncome | Age_disc_labels | Age_disc | YearlyIncome_disc_labels | YearlyIncome_disc | |
|---|---|---|---|---|---|---|
| 142 | 52 | 80000 | Bin_1 | (36.999, 58.0] | Bin_2 | (50000.0, 90000.0] |
| 122 | 59 | 110000 | Bin_2 | (58.0, 79.0] | Bin_3 | (90000.0, 130000.0] |
| 80 | 49 | 90000 | Bin_1 | (36.999, 58.0] | Bin_2 | (50000.0, 90000.0] |
| 33 | 69 | 20000 | Bin_2 | (58.0, 79.0] | Bin_1 | (9999.999, 50000.0] |
| 19 | 39 | 210000 | Bin_1 | (36.999, 58.0] | Bin_5 | (170000.0, 210000.0] |
| 54 | 59 | 70000 | Bin_2 | (58.0, 79.0] | Bin_2 | (50000.0, 90000.0] |
| 50 | 50 | 130000 | Bin_1 | (36.999, 58.0] | Bin_3 | (90000.0, 130000.0] |
| 93 | 72 | 70000 | Bin_2 | (58.0, 79.0] | Bin_2 | (50000.0, 90000.0] |
| 148 | 52 | 130000 | Bin_1 | (36.999, 58.0] | Bin_3 | (90000.0, 130000.0] |
| 45 | 66 | 30000 | Bin_2 | (58.0, 79.0] | Bin_1 | (9999.999, 50000.0] |
Дискретизацията е начин, чрез който можем да се справим с отличителните стойности, като те се поставят в най-ниския и най-високия интервал. В нашия пример те са сложени в Bin_5. Така тези стойности не се различават от останалите. След извършване на дискретизация тези променливи трябва да бъдат третирани като категорийни.
Поставяне на горен и долен праг и заместване с минимална и максимална допустима стойност
Този метод позволява обработка на отличителните стойности без да се премахват записи от извадката, но може да изкриви разпределението и връзката между отделните променливи.
# Намиране на интерквартилния размах
IQR_income = df['YearlyIncome'].quantile(0.75) - df['YearlyIncome'].quantile(0.25)
IQR_age = df['Age'].quantile(0.75) - df['Age'].quantile(0.25)
# Окриване на долната и горната граница
lower_boundary_income = df['YearlyIncome'].quantile(0.25) - (IQR_income * 1.5)
upper_boundary_income = df['YearlyIncome'].quantile(0.75) + (IQR_income * 1.5)
lower_boundary_age = df['Age'].quantile(0.25) - (IQR_age * 1.5)
upper_boundary_age = df['Age'].quantile(0.75) + (IQR_age * 1.5)
# Заместване с минималната и максималната допустима стойност
df['Age']= np.where(df['Age'] > upper_boundary_age, upper_boundary_age,
np.where(df['Age'] < lower_boundary_age, lower_boundary_age, df['Age']))
df['YearlyIncome']= np.where(df['YearlyIncome'] > upper_boundary_income, upper_boundary_income,
np.where(df['YearlyIncome'] < lower_boundary_income, lower_boundary_income, df['YearlyIncome']))Диаграмите тип кутия след прилагане на метода:
При този пример не се забелязва промяна в медианите и на двете променливи след прилагане на метода. Остават стойностите 70000 при YearlyIncome и 57 при Age.
Каква е ползата от обработката на отличителни стойности?
Идентификацията и обработката на отличителни стойности от извадката е ключов момент при изграждане на модели за машинно обучение. Такива стойности могат да създадат проблеми при работата на алгоритмите, като изкривят получените от тях резултати. Обработката на отличителни стойности по подходящ начин позволява получаването на по-високи стойности на метриките за оценка на работата на моделите, което води и до по-добро цялостно представяне на самия модел.
Искате да научите повече за машинното обучение?
Включете се в курса по машинно обучение и анализ на данни с Python.
Автор: Десислава Христова