Понятието регресия е много популярно и доста често, когато го чуем, веднага в ума ни изкача мисълта за статистическо моделиране и така наречения регресионен анализ. Значението на регресията от статистическа гледна точка е да се установят зависимости между признаците и да се определи каква е значимостта на връзката им.
При машинното обучение понятието регресия често е свързано с предвиждане на стойности на количествени характеристики на базата на вече известни данни за целевата променлива. Чрез регресионните алгоритми се прогнозират стойностите, като моделът може да връща отговорите с определена грешка.
Чрез тази статия бих искала да ви запозная с основна информация за регресията, като ще се фокусираме върху това какво представлява и какво е приложението ѝ в машинното обучение.
Типове регресия
Съществуват най-различни регресионни методи за предвиждане на стойности, като някои от най-често използваните са:
Линейна регресия
Линейната регресия е лесен и популярен подход при контролираното машинно обучение. Може да бъде единична или множествена в зависимост от броя на независимите променливи.
Единичната (обикновена) линейна регресия описва линейната зависимост между независимата променлива x и зависимата променлива у (y = f(x)).
Функцията има следния вид:
y = \beta_{0} + \beta_{1}x + \varepsilon, като
y – зависимата променлива
\beta_{0} – пресечна точка с оста y (intercept),
\beta_{1} – наклон (slope)
x – независимата променлива
\varepsilon – случайна грешка
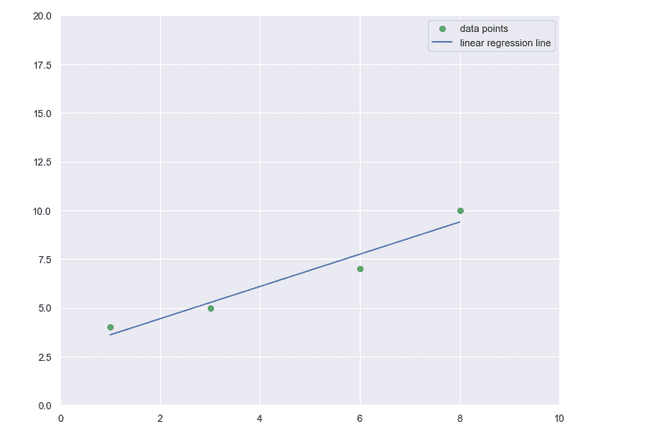
Единичната (обикновена) линейна регресия
Изготвено с Matplotlib: Python plotting
Най-простият модел на зависимостта между две променливи, измервани на интервалната скала, е правата линия. Наклонът ѝ показва с колко единици се изменя y при единица изменение на x.
Множествената линейна регресия дава възможност да анализираме влиянието на две или повече независими променливи върху една зависима променлива.
Функцията изразяваща връзката между x_{i} и y.
y = \beta_{0} + \beta_{1}x_{1} + \beta_{2}x_{2} + \cdots + \beta_{p}x_{p} + \varepsilon
Тук \beta_{1}, \beta_{2} и т.н. се наричат регресионни коефициенти и показват връзката между y и този x, пред който се намира съответният коефициент.
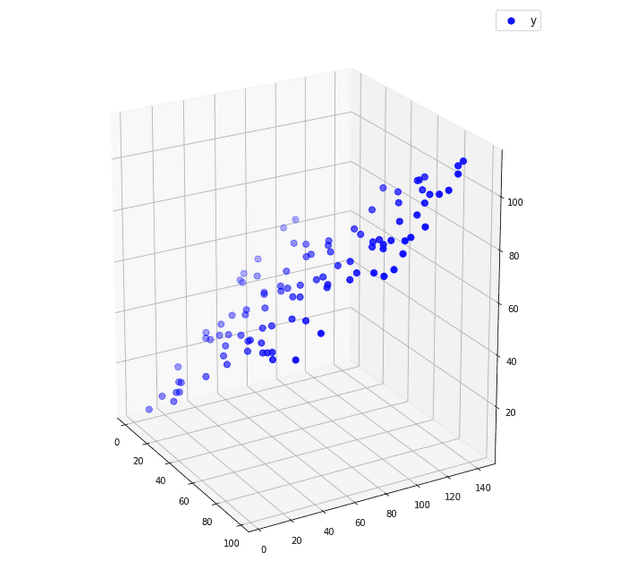
Множествената линейна регресия
Изготвено с Matplotlib: Python plotting
Как да определим стойността на коефициентите?
Това лесно може да стане чрез метода на най-малките квадрати (Least Squared Method). Сумират се разликите между действителните и прогнозираните стойности (грешката на предвиждането), повдигнати на квадрат, като се подбират тези стойности на коефициентите, при които сумата на квадратите е минимална. Грешката на предвиждането е разстоянието между дадената точка и регресионната линия. Причината да се взимат квадратите е за да няма отрицателни стойности, които да доведат до нулева стойност на грешката. Така ще получим оптималните параметри и тази линия, която е най-близка до точките.
Логистична регресия
Друг популярен тип регресия е логистичната, но тя се използва за класификация. При нея зависимата променлива има само две възможни стойности (е дихотомна), като моделът пресмята вероятността y да принадлежи към една от две категории в зависимост от стойността на x. Задава се праг (threshold) със стойност между 0 и 1, според който обектът да бъде класифициран.
Например ако сложим праг 0.5, всичко, което е с вероятност над тази граница спада към едната категория, а ако е под, е в другата категория.
Използва се логистичната (сигмоидната) функция, която има следният вид:
P = \frac{1}{1 + e^{-y}}Тук y е регресионното уравнение.
Независимо каква стойност имаме за y, сигмоидната функция ще върне резултат между 0 и 1.
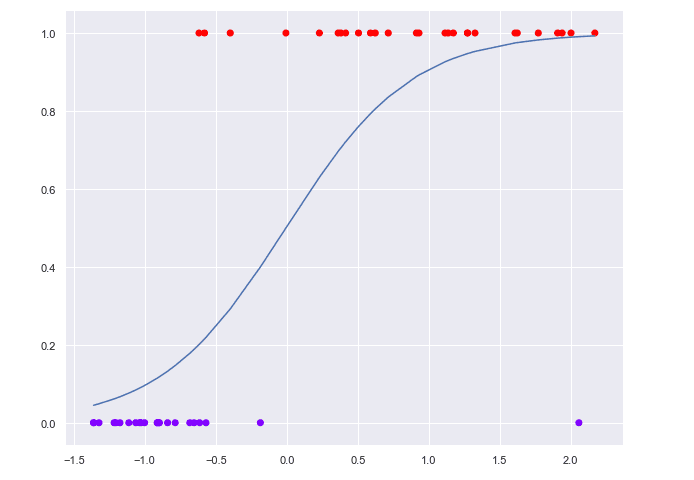
Логистична регресия
Изготвено с Matplotlib: Python plotting
При логистичната регресия не се използва методът на най-малките квадрати, за да се определят стойностите на параметрите, а вместо това се използва методът на максималното правдоподобие, чрез който се избират такива параметри, при които да има максимална вероятност.
Полиномна регресия
Това е форма на линейна регресия, при която имаме полиноми в регресионния модел. Използва се, когато права линия не изразява достатъчно добре връзката между данните. При този тип регресия имаме две или повече независими променливи и една зависима.
Функцията изглежда по следния начин:
y = \beta_{0} + \beta_{1}x + \beta_{2}x^{2} + \beta_{3}x^{3} + \cdots + \beta_{p}x^{p} + \varepsilonРазликата с линейната регресия е че x се повдига на степен и съответно кривата има по-сложен характер в зависимост от степента.
За определяне на коефициентите можем да използваме метода на най-малките квадрати също както при линейната регресия.
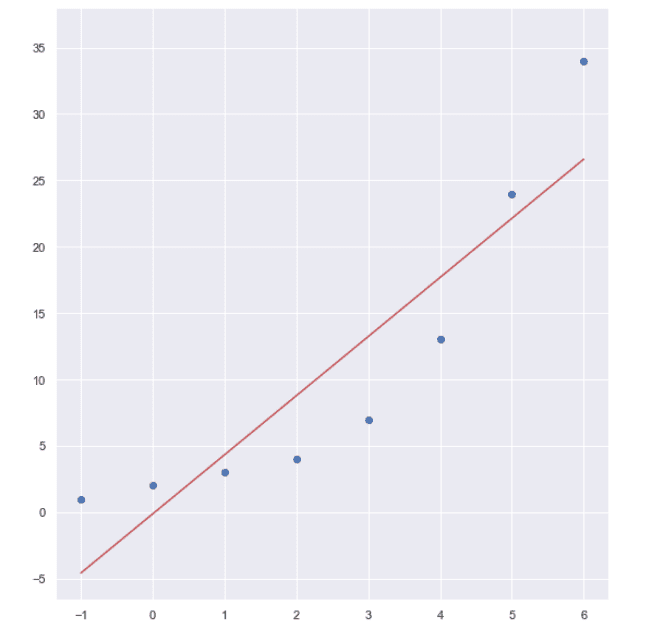
Линейна регресия
Изготвено с Matplotlib: Python plotting
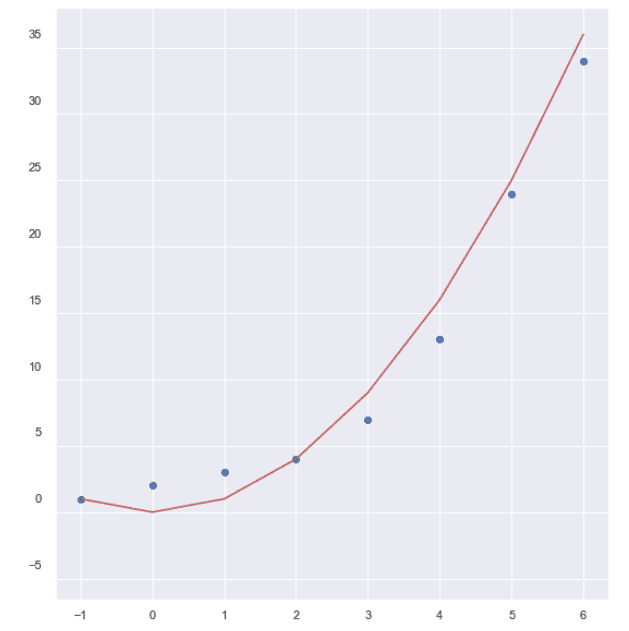
Полиномна регресия
Изготвено с Matplotlib: Python plotting
На изображенията са представени кривите на линейната и полиномната регресия. Използвани са синтетични данни за този пример и ясно се вижда, че правата линия не е подходяща за разлика от кривата на полиномната регресия, която добре изразява връзката между данните.
При какви задачи се използва регресия?
Линейна и полиномна регресия може да се прилагат за пронозиране на:
- стойности на заплати на служители
- продажби на фирмата
- качество на вино и др.
Логистична регресия се използва например ако искаме да разберем дали:
- клиент ще закупи или не съответен продукт
- кандидат ще спечели или не избори
- ще има или не земетресение в съответен ден и др.
След задълбочен анализ се определя кой регресионен модел е подходящ за данните, които искаме да анализираме. Например, ако връзката между променливите не е линейна, трябва да се използва модел на нелинейна регресия (полиномна или др.), която правилно да опише връзката между данните, за да може да получим точни резултати.
Как се оценява качеството на модела?
Оценяваме качеството на модела чрез коефициент на детерминация R2 или още наричан R-квадрат. Той изразява колко е силна зависимостта между променливите в проценти, като показва какъв процент от вариацията на една променлива може да бъде обяснена с вариацията на друга.
Също добри оценки на качеството на модела са:
- Средна абсолютна грешка (Mean Absolute Error)
MAE = \frac{1}{n} \sum_{i=1}^{n} \left | y_{i} - {y}'_{i} \right |- Средна квадратична грешка (Mean Squared Error)
MSE = \frac{1}{n} \sum_{i=1}^{n} (y_{i} - {y}'_{i})^{2}- Средна абсолютна процентна грешка (Mean Absolute Percentage Error)
MAPE = \frac{1}{n} \sum_{i=1}^{n} \frac{\left |y_{i} - {y}'_{i} \right |}{\left |y_{i} \right |} * 100Чрез библиотеката Scikit-learn за анализ на данни и машинно обучение с Python можем лесно да изчисляваме тези метрики.
С какво е полезна регресията в машинното обучение?
При машинното обучение регресията има много широко приложение. Тя е нещо основно и добре изучено. Получават се добри резултати чрез използване на регресионните алгоритми, като те са подходящи за бързи изчисления и прогнозите са достатъчно точни. Освен за превиждане на стойности, регресията в машинното обучение може да бъде използвана и при подготовката на данните – ако имаме липсващи стойности, да се определи евентуално какви биха били те. Като цяло всеки, който навлиза в областта на машинното обучение, трябва да бъде запознат с регресията и нейните особености.
Искате да научите повече за машинното обучение?
Включете се в курса по машинно обучение и анализ на данни с python.
Автор: Десислава Христова