Как влияят данните със стойности от различен порядък?
В повечето случаи извадките съдържат независими променливи със стойности, които са от различен порядък. Това може да повлияе негативно върху работата на модела за машинно обучение. Например, ако имаме ръст и тегло на хора и искаме да изградим модел, чрез който да предскажем кое място ще спечелят на състезание.
| Name | Height | Weight | Result | |
|---|---|---|---|---|
| 0 | Steve Harrison | 1.85 | 96 | 2 |
| 1 | James Douglas | 1.72 | 81 | 1 |
| 2 | Vicky McNickol | 1.58 | 65 | 3 |
От таблицата веднага се вижда, че ръстът, измерен в метри, съдържа доста по-малки стойности от теглото, което е в килограми. Mоделът в този случай може да определи, че теглото е по-важно при разпределяне на хората в съответните класове.
Нужно е да се извършат необходимите трансформации, така че стойностите да бъдат от еднакъв порядък. Тази техника се нарича мащабиране на характеристики (Feature scaling) и се прилага в етапа на предварителната обработка на данните (Data preprocessing).
Защо се мащабират данните и каква е разликата в получените резултати?
При работа на определени модели с немащабирани данни, например при такива, които изчисляват коефициенти, получаваме резултати с голяма грешка. За всяка характеристика се изчисляват теглови коефициенти и мащабирането се прилага, защото в противен случай моделът може да определи някоя променлива за по-важна от друга, ако тя съдържа по-високи стойности.
Например, ако имаме месечен доход, чиито стойности попадат в интервал над 1000, и характеристиката възраст, при която 85 години е максимумът. В такива случаи моделът може да прецени, че доходът е по-важен, а в действителност да не е така.
Кои алгоритми за машинно обучение изискват данните да бъдат мащабирани?
- Алгоритми, изчисляващи разстояние:
- k най-близки съседи (k-Nearest Neighbors)
- Метод на опорните вектори (Support Vector Machines)
- k-means клъстеризация (k-means clustering)
- Алгоритми, изчисляващи коефициенти:
- Регресионни алгоритми (логистична регресия, линейна, нелинейна и др.)
- Невронни мрежи
Алгоритмите, които изискват работа с мащабирани данни, не се изчерпват до тук. Има и още много други като например PCA, SVD, Factorization Machines и други, които участват в различните етапи при изграждането на модела.
В тази статия ще ви запозная с някои от ключовите методи, чрез които се прилага мащабирането на данни.
Начини за мащабиране
Библиотеката Scikit-learn на Python съдържа в модула си за предварителна обработка на данните (preprocessing) различни методи, чрез които се мащабират данни.
За примерите, които ще видите по-надолу в статията, са използвани синтетични данни за служители, съдържащи 8 записа, в които има информация за тяхното име, възраст и заплата.
df = pd.DataFrame({'Name': ['Oliver Hamilton', 'Jake Smith', 'Jordan Todosey', 'Kim Steele', 'Kevin Lang', 'Victoria Ong', 'Victor Rasmussen','Jessica Scott'],
'Age': [18, 35, 28, 41, 60, 44, 24, 55],
'Salary': [3400, 1400, 1600, 2550, 850, 1780, 1250, 1000]})Резултат:
| Name | Age | Salary | |
|---|---|---|---|
| 0 | Oliver Hamilton | 18 | 3400 |
| 1 | Jake Smith | 35 | 1400 |
| 2 | Jordan Todosey | 28 | 1600 |
| 3 | Kim Steele | 41 | 2550 |
| 4 | Kevin Lang | 60 | 850 |
| 5 | Victoria Ong | 44 | 1780 |
| 6 | Victor Rasmussen | 24 | 1250 |
| 7 | Jessica Scott | 55 | 1000 |
Характеристиките, които трябва да бъдат мащабирани са Age и Salary. Ще отделим стойностите им в масив, върху който след това ще приложим различните методи.
features = df.iloc[:,[1,2]].values
features
Output:
array([[ 18, 3400],
[ 35, 1400],
[ 28, 1600],
[ 41, 2550],
[ 60, 850],
[ 44, 1780],
[ 24, 1250],
[ 55, 1000]], dtype=int64)StandardScaler
Библиотеката Scikit-learn притежава метод, наречен StandardScaler(), чрез който данните могат да бъдат стандартизирани. Използва се при алгоритми, които очакват входните данни да имат стандартно нормално разпределение и работят по-добре с мащабирани стойности (линейна и логистична регресия, линеен дискриминантен анализ и др.). След като той бива приложен, формата на разпределението не се променя, средната стойност на всички независими променливи става равна на 0, а стандартното отклонение е 1.
Ако данните не са преминали през стандартизация, променлива с висока дисперсия (variance) ще оказва повече влияние върху работата на модела и бихме получили резултати с по-голяма грешка.
Формула:
\frac{X_{i} - \mu}{\sigma}При стандартизацията данните са трансформирани чрез изваждане на средната стойност и разделяне на стандартното отклонение.
Пример:
ss = StandardScaler()
standardized = ss.fit_transform(features)
standardized
Output:
array([[-1.45864213, 2.08757736],
[-0.22649723, -0.41064536],
[-0.73385101, -0.16082309],
[ 0.20837745, 1.02583271],
[ 1.58548058, -1.09765661],
[ 0.42581478, 0.06401696],
[-1.02376746, -0.59801206],
[ 1.22308502, -0.9102899 ]])Резултат:
| Name | Age | Salary | |
|---|---|---|---|
| 0 | Oliver Hamilton | -1.45864 | 2.08758 |
| 1 | Jake Smith | -0.226497 | -0.410645 |
| 2 | Jordan Todosey | -0.733851 | -0.160823 |
| 3 | Kim Steele | 0.208377 | 1.02583 |
| 4 | Kevin Lang | 1.58548 | -1.09766 |
| 5 | Victoria Ong | 0.425815 | 0.064017 |
| 6 | Victor Rasmussen | -1.02377 | -0.598012 |
| 7 | Jessica Scott | 1.22309 | -0.91029 |
MinMaxScaler
MinMaxScaler() трансформира стойностите на променливите в определен интервал, който по подразбиране е между 0 и 1. Този метод не променя формата на разпределението и не намаля влиянието на силно отличаващите се стойности. Прилага се при ключови алгоритми за оптимизация като градиентно спускане (gradient descent), при такива, които поставят тегла на променливите (невронни мрежи и регресия) и при алгоритми, които изчисляват разстояние (k най-близки съседи).
Формула:
\frac{X_{i} - X_{min}}{X_{max} - X_{min}}При MinMaxScaler() се изважда минималната стойност и полученото се разделя на размаха (max-min).
Пример:
mm = MinMaxScaler()
minmaxed = mm.fit_transform(features)
minmaxed
Output:
array([[0. , 1. ],
[0.4047619 , 0.21568627],
[0.23809524, 0.29411765],
[0.54761905, 0.66666667],
[1. , 0. ],
[0.61904762, 0.36470588],
[0.14285714, 0.15686275],
[0.88095238, 0.05882353]])Резултат:
| Name | Age | Salary | |
|---|---|---|---|
| 0 | Oliver Hamilton | 0 | 1 |
| 1 | Jake Smith | 0.404762 | 0.215686 |
| 2 | Jordan Todosey | 0.238095 | 0.294118 |
| 3 | Kim Steele | 0.547619 | 0.666667 |
| 4 | Kevin Lang | 1 | 0 |
| 5 | Victoria Ong | 0.619048 | 0.364706 |
| 6 | Victor Rasmussen | 0.142857 | 0.156863 |
| 7 | Jessica Scott | 0.880952 | 0.0588235 |
RobustScaler
RobustScaler() методът е подходящ, когато искаме да намалим влиянието на силно отличаващите се стойности. Тази трансформация не променя формата на разпределението и прави така, че стойностите да бъдат в определен мащаб, който не е предварително зададен както е при MinMaxScaler().
Формула:
\frac{X_{i} - Q2}{Q3 - Q1}При RobustScaler() се изважда медианата (Q2) и полученият резултат се разделя на интерквартилния размах (Q3 – Q1).
Пример:
rs = RobustScaler()
robusted = rs.fit_transform(features)
robusted
Output:
array([[-1.01265823, 2.42038217],
[-0.15189873, -0.12738854],
[-0.50632911, 0.12738854],
[ 0.15189873, 1.33757962],
[ 1.11392405, -0.82802548],
[ 0.30379747, 0.3566879 ],
[-0.70886076, -0.31847134],
[ 0.86075949, -0.63694268]])Резултат:
| Name | Age | Salary | |
|---|---|---|---|
| 0 | Oliver Hamilton | -1.01266 | 2.42038 |
| 1 | Jake Smith | -0.151899 | -0.127389 |
| 2 | Jordan Todosey | -0.506329 | 0.127389 |
| 3 | Kim Steele | 0.151899 | 1.33758 |
| 4 | Kevin Lang | 1.11392 | -0.828025 |
| 5 | Victoria Ong | 0.303797 | 0.356688 |
| 6 | Victor Rasmussen | -0.708861 | -0.318471 |
| 7 | Jessica Scott | 0.860759 | -0.636943 |
MaxAbsScaler
Методът MaxAbsScaler() мащабира данните за всяка променлива по нейната максимална абсолютна стойност. Той не променя вида на разпределението и след прилагането му, при всяка характеристика максималната абсолютна стойност става равна на 1, а интервалът е между 0 и 1. Също както при MinMaxScaler(), методът не намаля влиянието на силно отличаващите се стойности.
Формула:
\frac{X_{i}}{X_{max}}Трансформацията се случва, като всяка точка се разделя на максималната абсолютна стойност за съответната променлива.
Пример:
mxas = MaxAbsScaler()
maxabs = mxas.fit_transform(features)
maxabs
Output:
array([[0.3 , 1. ],
[0.58333333, 0.41176471],
[0.46666667, 0.47058824],
[0.68333333, 0.75 ],
[1. , 0.25 ],
[0.73333333, 0.52352941],
[0.4 , 0.36764706],
[0.91666667, 0.29411765]])Резултат:
| Name | Age | Salary | |
|---|---|---|---|
| 0 | Oliver Hamilton | 0.3 | 1 |
| 1 | Jake Smith | 0.583333 | 0.411765 |
| 2 | Jordan Todosey | 0.466667 | 0.470588 |
| 3 | Kim Steele | 0.683333 | 0.75 |
| 4 | Kevin Lang | 1 | 0.25 |
| 5 | Victoria Ong | 0.733333 | 0.523529 |
| 6 | Victor Rasmussen | 0.4 | 0.367647 |
| 7 | Jessica Scott | 0.916667 | 0.294118 |
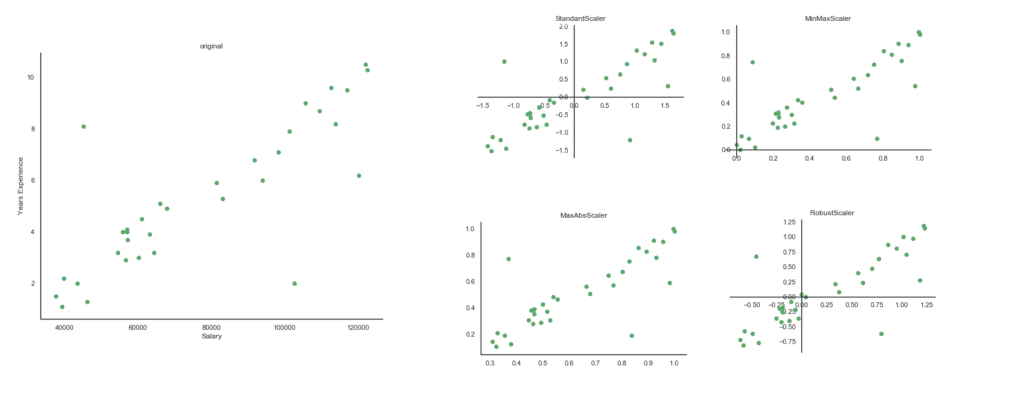
Обобщена визуализация, показваща разликите при мащабиране с различните методи
За изготвянето на визуализацията, която ще видите по-надолу, е използвана извадката Salary_Data, която можете да изтеглите от тук.
В нея има 33 записа, съдържащи информация за трудов стаж и заплати на служители.
Първите 5 реда от извадката изглеждат по следния начин:
| YearsExperience | Salary | |
|---|---|---|
| 0 | 1.1 | 39343 |
| 1 | 1.3 | 46205 |
| 2 | 1.5 | 37731 |
| 3 | 2 | 43525 |
| 4 | 2.2 | 39891 |
Променливата YearsExperience съдържа доста по-малки стойности, като максималната е 10.5, а при Salary са много по-високи и максимумът е 122391.
Веднага се забелязва, че зависимостта между двете променливи е положителна и възходяща и че четирите метода не променят формата на разпределението. Това, което е различно, е интервалът, в който попадат стойностите след трансформацията. При MinMaxScaler() и MaxAbsScaler() е между 0 и 1, докато при другите два метода, е малко по-голям. Когато стойностите са трансформирани чрез StandardScaler(), минималната стойност е -1.5, а максималната е 1.9. При RobustScaler() са съответно -0.8 и 1.2.
На диаграмите се забелязват и 3 необичайни стойности (outliers). Единствено ако данните са мащабирани чрез RobustScaler(), то тогава те няма да оказват влияние върху получените от модела резултати. Останалите 3 метода не намаляват влиянието на такива стойности.
Каква е ползата от мащабирани данни?
Когато данните са мащабирани, всички характеристики са равнопоставени, т.е. липсва склонността алгоритъмът да възприема една променлива за по-значима от друга. Това въздейства положително върху работата на модела, като се подобряват финалните резултати и имаме възможността да направим по-точна оценка на качеството.
Искате да научите повече за машинното обучение?
Включете се в курса по машинно обучение и анализ на данни с Python.
Автор: Десислава Христова