Machine Learning: Метрики за оценка на регресионни модели

Регресионните модели се използват за решаване на различни задачи, при които целевата променлива е числова и непрекъсната величина (например заплата, цена, тегло и др.). Целта е на базата на известни характеристики, които са независими променливи, да се прогнозира каква би била стойността на целевата променлива, като оценката е с определена грешка в допустими граници.

Кои са някои от по-често използваните регресионни алгоритми?

• Linear Regression
• Lasso & Ridge Regression
• Decision Tree Regressor
• Random Forest Regressor
• k-Nearest Neighbors (KNN) Regressor
• Support Vector Regressor (SVR)
• Stochastic Gradient Descent Regressor

Как да оценим регресионни модели?

Когато изградим един модел, е необходимо да проверим колко добре работи той. За оценка на неговото качество можем да вземем под внимание стойностите на различни метрики – коефициент на детерминация, средна абсолютна грешка, средна квадратична грешка и други.

В тази статия ще разгледаме различните метрики за оценка на регресионни модели в контекста на практически пример. Ще използваме извадка, която има 206 обекта и 26 колони. Тя съдържа данни за автомобили (тип двигател, брой врати, дължина и ширина на колата и др.), на базата на които трябва да се прогнозира цената. При изграждане на регресионния модел ще бъдат използвани 3 метода – линейна регресия (Linear Regression), случайна гора (Random Forest Regressor), и стохастично градиентно спускане (Stochastic Gradient Descent Regressor).

В примера ще се фокусираме само върху метриките за оценка на регресионните модели. Поради тази причина данните са предварително изчистени, т.е. премахнати са ненужни колони, отличителни (екстремни) стойности, кодирани са категорийни променливи и т.н.

Ако искате да научите повече за някои конкретни стъпки от етапа на предварителната подготовка на данните, можете да прочетете в съответните статии:

• Machine Learning: Как да обработим липсващи стойности при подготовката на данни за анализ?
• Machine Learning: Как да се справим с отличителни стойности (outliers)?
• Machine Learning: Защо е важно данните да са мащабирани?
• Machine Learning: Силата на визуализацията на данни. Коя графика какво ни показва?
• Machine Learning: Интерактивни визуализации с Python
• Machine Learning: Какво означава извадката да не е балансирана?

Примера, който ще разгледаме по-надолу, можете да изтеглите от тук.

1) R-квадрат & Изравнен R-квадрат

• Коефициент на детерминация – R-квадрат (R-squared)

Коефициентът на детерминация показва до колко добре стойностите на целевата променлива се определят от модела при постъпване на нови данни. Това е статистическа метрика, която ни дава информация за това какъв процент от дисперсията на целевата променлива се прогнозира чрез стойностите на независимите променливи.

Формула:

R^{2} = 1 - \frac{\sum_{i = 1}^{n} \left ( y_{i}- \hat{y_{i}} \right )^{2}}{\sum_{i = 1}^{n} \left ( y_{i} - \bar{y} \right )^{2}}

• yi – действителните стойности
• ŷi – прогнозираните стойности
• ȳ – средната стойност на целевата променлива
• (yi – ŷi) – грешка на оценката

Като използваме библиотеката Scikit-learn на Python, можем да намерим R-квадрат по 2 начина. Единият е чрез функцията r2_score() от модула metrics, а другият е чрез метода score(), който има всеки от изградените модели, като получените резултати от тях са еднакви. Разликата се състои в това, че имат различни параметри. При r2_score() подаваме действителните и прогнозираните стойности на целевата променлива, докато score() получава като параметри стойностите на независимите характеристики и действителните стойности на целевата променлива и не е нужно преди това да сме извикали predict(), тъй като методът вътрешно го прави, след което сравнява действителните и прогнозираните стойности.

# Изчисляване на R-квадрат за отделните модели и запазване в променливи
lr_score = r2_score(y_test, y_pred_lr)
rf_score = r2_score(y_test, y_pred_rf)
sgd_score = r2_score(y_test, y_pred_sgd)

Резултат:

	Model	R2_score
0	LinearRegression	0.872407
1	RandomForestRegressor	0.927413
2	SGDRegressor	0.874054

Методите, използващи Linear Regression и SGD имат R-квадрат с почти еднакви стойности приблизително 0.87, т.е. 87% от дисперсията на цената се обяснява от стойностите на независимите променливи. Резултатът при Random Forest е най-висок – 93%.

Изравнен коефициент на детерминация – Изравнен R-квадрат (Adjusted R-squared)

Метриката изравнен R-квадрат има същото предназначение като R-квадрат, но за разлика от нея взима под внимание общия брой обекти в извадката и зачита само тези характеристики, които имат значително влияние върху дисперсията на целевата променлива.

Изравненият R-квадрат е винаги по-малък или равен на R-квадрат, тъй като R-квадрат се увеличава всеки път, когато се добави нова характеристика. Двете метрики са равни, когато има само една независима променлива.

Формула:

 Adjusted\;R^{2} = 1 - \frac{\left ( 1 - n \right )}{[n - \left ( k + 1 \right )]} \left ( 1 - R^{2} \right )  

• n – общият брой обекти
• k – брой независими променливи

В Scikit-learn няма конкретна функция, с която да се изчисли изравненият R-квадрат, затова ще напишем наша собствена.

# Дефиниране на функция, която изчислява изравнен R-квадрат
def adj_r2(r2, y_test, X_test):
    return 1 - (1-r2)*(y_test.size-1)/(y_test.size-X_test.shape[1]-1)

# Изчисляване на изравнен R-квадрат за отделните модели и запазване в променливи
adj_r_squared_lr = adj_r2(lr_score, y_test, X_test)
adj_r_squared_rf = adj_r2(rf_score, y_test, X_test)
adj_r_squared_sgd= adj_r2(sgd_score, y_test, X_test)

Резултат:

	Model	Adj_R2
0	LinearRegression	0.834401
1	RandomForestRegressor	0.905792
2	SGDRegressor	0.836538

В нашия случай разликата между стойностите на R-квадрат и изравнен R-квадрат за отделните методи не е толкова голяма – между 2-4%, като отново Random Forest е с най-висок резултат – 91%.

Метриките R-квадрат и изравнен R-квадрат не дават информация за това точно колко прогнозираните стойности се разминават с реалните. За тази цел е необходимо да се направи проверка и с останалите метрики за оценка на регресионни модели – обща
абсолютна грешка (MAE), средна абсолютна процентна грешка (MAPE), средна квадратична грешка (MSE) и корен от средната квадратична грешка (RMSE).

2) Средна абсолютна грешка (MAE) и Средна абсолютна процентна грешка (MAPE)

• MAE

Тази метрика показва с колко средно се различават определените от модела стойности с тези, които са в действителност. Предимството ѝ е това, че резултатите, които се получават, са в същите единици като целевата променлива и не се влие толкова много от наличието на екстремни стойности в извадката.

Формула:

MAE = \frac{1}{n} \sum_{i = 1}^{n}\left | y_{i} - \hat{y_i} \right |

yi – действителните стойности
ŷi – прогнозираните стойности
(yi – ŷi) – грешка на оценката

В Scikit-learn има функция mean_absolute_error() от модула metrics, чрез която можем да намерим MAE.

# Изчисляване на MAE за отделните модели и запазване в променливи
lr_mae = mean_absolute_error(y_test, y_pred_lr)
rf_mae = mean_absolute_error(y_test, y_pred_rf)
sgd_mae = mean_absolute_error(y_test, y_pred_sgd)

Резултат:

	Model	MAE
0	LinearRegression	2104.39
1	RandomForestRegressor	1488.58
2	SGDRegressor	1987.59

От таблицата можем да установим, че и трите модела се справят сравнително добре. Средната цена за автомобил е 13276.71, така че грешка от около 1500-2500 долара може да е приемлива (моделът може допълнително да се оптимизира, за да се намали тази грешка). Random Forest има най-ниска стойност за MAE, но не се различава толкова много от тази при останалите модели.

• MAPE

Средната абсолютна процентна грешка е статистическа метрика, която се измерва в проценти и показва относителната стойност на отклоненията.

Формула:

MAPE = \frac{1}{n}\sum_{i=1}^{n}\frac{\left | y_{i} - \hat{y_{i}} \right |}{\left | y_{i} \right |} * 100

• n – общият брой обекти
• yi – действителните стойности
• ŷi – прогнозираните стойности
• (yi – ŷi) – грешка на оценката

Тази метрика се интерпретира по-лесно отколкото MAE. Например, по-разбираемо е, когато се каже, че определените от модела стойности се различават от действителните с 4% отколкото с 3000 единици.

В Scikit-learn няма конкретна функция, чрез която да изчислим тази метрика, затова отново ще дефинираме наша собствена.

# Дефиниране на функция, която изчислява MAPE
def mape(y_true,y_pred):
    return np.mean( np.abs((y_true - y_pred)/y_true ) ) * 100

# Изчисляване на MAPE за отделните модели и запазване в променливи
mape_lr = mape(y_test, y_pred_lr)
mape_rf = mape(y_test, y_pred_rf)
mape_sgd = mape(y_test, y_pred_sgd)

Резултат:

	Model	MAPE
0	LinearRegression	15.20
1	RandomForestRegressor	10.60
2	SGDRegressor	14.18

Стойностите за MAPE при трите модела са между 10% и 20%, което ги прави значително добри според интерпретацията на C. D. Lewis в книгата Industrial and business forecasting methods: a practical guide to exponential smoothing and curve fitting. Random Forest е с най-нисък процент на грешката – 10.60%.

3) Средна квадратична грешка (Mean Squared Error) & Корен от средната квадратична грешка (Root Mean Squared Error)

• MSE

Тази метрика представлява средната стойност на квадратите на грешката на оценката и е винаги с положителни стойности. Влияе се много от наличието на екстремни стойности в извадката, тъй като повдигането на квадрат увеличава още повече тежестта им.

Формула:

MSE = \frac{1}{n} \sum_{i = 1}^{n}\left ( y_{i} - \hat{y_i} \right )^2

• n – общият брой обекти
• yi – действителните стойности
• ŷi – прогнозираните стойности
• (yi – ŷi) – грешка на оценката

В Scikit-learn има функция mean_squared_error() от модула metrics, чрез която можем да изчислим MSE.

# Изчисляване на MSE за отделните модели и запазване в променливи
lr_mse = mean_squared_error(y_test, y_pred_lr)
rf_mse = mean_squared_error(y_test, y_pred_rf)
sgd_mse = mean_squared_error(y_test, y_pred_sgd)

Резултат:

	Model	MSE
0	LinearRegression	8981258.50
1	RandomForestRegressor	5109382.45
2	SGDRegressor	8865327.71

Получените резултати са с много високи стойности, но да не забравим, че грешката е на квадрат. Това е и един от недостатъците на тази метрика. Не става много ясно с колко реално е разминаването, когато стойностите са в квадратни единици.

• RMSE

По-често в практиката се взима коренът на MSE, тъй като е в същите единици като целевата променлива. Има много общо с MAE и доста често биват сравнявани двете метрики. RMSE се влияе повече от екстремни стойности в извадката за разлика от MAE.

Формула:

RMSE = \sqrt{\frac{1}{n} \sum_{i = 1}^{n}\left ( y_{i} - \hat{y_i} \right )^2}

• n – общият брой обекти
• yi – действителните стойности
• ŷi – прогнозираните стойности
• (yi – ŷi) – грешка на оценката

Можем да намерим корена на MSE чрез функцията sqrt() на библиотеката NumPy и като параметър подадем променливите, в които сме запазили стойностите на MSE за всеки от моделите.

# Изчисляване на RMSE за отделните модели и запазване в променливи
rmse_lr = np.sqrt(lr_mse)
rmse_rf = np.sqrt(rf_mse)
rmse_sgd = np.sqrt(sgd_mse)

Резултат:

	Model	RMSE
0	LinearRegression	2996.87
1	RandomForestRegressor	2260.39
2	SGDRegressor	2977.47

От таблицата можем да видим, че моделите, използващи Linear Regression и SGD имат много малка разлика в стойностите на RMSE. При Random Forest отново е най-ниска, но се различава с тези на останалите модели само с около 700 долара.

Обобщение

Резултатите от всички оценки можете да видите в следната обобщаваща таблица:

	Model	R2_score	Adj R2	MSE	RMSE	MAE	MAPE
0	LinearRegression	0.87	0.83	8981258.50	2996.87	2104.39	15.20
1	RandomForestRegressor	0.93	0.91	5109382.45	2260.39	1488.58	10.60
2	SGDRegressor	0.87	0.84	8865327.71	2977.47	1987.59	14.18

В нашия случай моделът, използващ метода Random Forest, има най-добри резултати по всички показатели.

• 

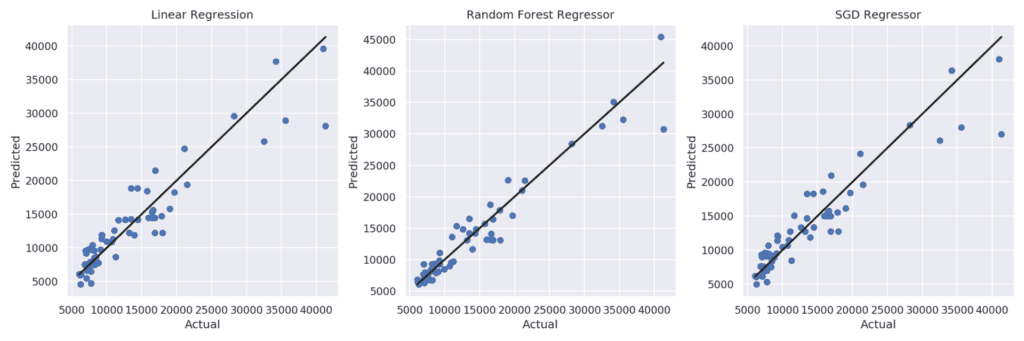
На графиката можете да видите диаграми на разсейването за всеки от моделите, съпоставящи стойностите, прогнозирани от регресора, с действителните. Черната линия съответства на идеален регресор, прогнозиращ със 100% точност.

При трите модела няма толкова голямо отклонение от действителните стойности при цени, които са между 5000 и 10000, но по-високите цени ги е прогнозирало с по-голяма грешка на оценката.

При методите, използващи Linear Regression и SGD, за цени, които са с по-ниски стойности, регресорите прогнозират, като предимно занижават цената, докато при Random Forest се забелязва баланс при завишените и занижените стойности, а в някои случаи дори и почти със 100% точност е направена прогнозата.

Следващата таблица съдържа 5 случайно взети реда и показва разликите между действителните и прогнозираните от моделите стойности.

	Actual	Logistic Regression	Random Forest Regressor	SGD Regressor
9	17859.20	14715.60	17805.30	15497.30
105	19699.00	18215.30	16824.10	18409.20
139	7053.00	9227.41	6598.80	9114.96
73	40960.00	39547.70	45400.00	38177.80
174	10698.00	10912.80	8809.73	10709.70

Изборът на правилния регресионен модел разбира се не зависи само от стойностите на метриките за оценка. Има и други фактори, които оказват влияние върху избора на подходящия модел като например бързината или обема данни. Въпреки че Random Forest дава най-добри резултати в нашия пример, при по-голям обем данни, работи по-бавно и изисква повече памет отколкото другите 2 метода. Linear Regression е доста бърз и лесен за разбиране метод, а SGD е много подходящ, ако искаме оценката да се даде на момента или извадката съдържа голям брой обекти и характеристики.

Кои метрики какво ни показват?

Метриките R-квадрат и изравнен R-квадрат позволяват да добием цялостна представа за това колко добре се справя моделът и да правим лесно сравнение с други модели, използващи различни алгоритми. Останалите метрики ни дават информация за това колко е голяма грешката на оценката. RMSE и MAE много често се взимат под внимание в практиката. Колкото по-близо са до 0, толкова по-добър е моделът. RMSE е винаги със стойност равна или по-голяма от MAE, защото дава повече тежест на по-големите грешки.

Коя метрика би ни дала по-добра представа за качеството на регресионния модел зависи от самата задача. Някои модели имат високи стойности за една метрика, но това не означава, че и за останалите метрики е така. Необходимо е да се разбере какво показва всяка и да се изберат тези, които са подходящи за съответната бизнес задача.

Искате да научите повече за машинното обучение?

Включете се в курса по машинно обучение и анализ на данни с Python.

Научете повече

Автор: Десислава Христова