Библиотеката Hyperopt е създадена специално за оптимизация на модели за машинно обучение и позволява бързо и лесно да открием кои са най-добрите параметри и техните стойности вместо да се опитваме да ги търсим чрез ръчни настройки.
В тази статия ще използваме Hyperopt, за да открием оптималните параметри на модел за машинно обучение в контекста на практическа задача и ще видим как се изменят резултатите след оптимизация.
Преглед на възможностите на библиотеката Hyperopt
Hyperopt използва Бейсовата оптимизация за откриване на оптималните параметри, т.е. подходът е вероятностен, като се преминава през пространство от параметри и техните стойности, за да се намери минимума на конкретна функция. За разлика от други методи като рандомизираното и решетъчното търсене на Scikit-learn, при Hyperopt се взимат под внимание предишни итерации, когато се търсят оптималнитe параметри.
Необходимо е да преминем през няколко стъпки, когато оптимизираме модел чрез библиотеката Hyperopt:
1/ Дефиниране на целевата функция
Целевата функция е тази, на която търсим минимума. Това често е функция на загубите (loss function). Например, ако искаме да намерим тези стойности на параметрите, при които средната квадратична грешка е най-ниска.
2/ Дефиниране на пространство от параметри и техните възможни стойности
Hyperopt предоставя много възможности за настройки на параметрите благодарение на функциите от модула hp. Поддържат се числови и нечислови стойности:
- Нечислови параметри - hp.choice()
- Цели числа - hp.randint(), hp.quniform(), hp.qloguniform() и hp.qlognormal()
- Дробни числа - hp.normal(), hp.uniform(), hp.lognormal() и hp.loguniform()
За цели и дробни числа може да се използва и hp.choice(), когато искаме да изберем една конкретна стойност от определени такива в списък.
Употребата на тези функции следва малко по-надолу в практическия пример.
3/ Инициализиране на Trials обекта
В Trials обекта се съхраняват всички резултати от извършеното търсене на оптимални параметри. Получаваме ги под формата на списък от речници.
- trials.trials - всички резултати от всяка една итерация
- trials.results - успешно изчислените стойности, получени от целевата функция и статуса на конкретната итерация (дали е успешна или не)
- trials.losses() - стойностите, получени от целевата функция
- trials.statuses() - статусите на всяка итерация
4/ Избор на оптимизационен алгоритъм, който да търси в пространството от параметри
Hyperopt предлага няколко варианта за оптимизационен алгоритъм, като основен е Tree Parzen Estimator (TPE). При него се изгражда вероятностен модел, който е базиран на теоремата на Бейс.
Формулата е следната:
p(y\mid x) = \frac{p(x\mid y) * p(y)}{p(x)}- p(y|x) е вероятността на резултата на целевата функция по отношение на параметрите
- p(x|y) е вероятността на параметрите по отношение на резултата на целевата функция
- p(x) e вероятността на параметрите
- p(y) e вероятността на резултата на целевата функция
Стойностите на параметрите се разделят на 2 части на базата на определен праг, с който се сравнява оценката на целевата функция. Едната част е l(x), където резултатите са хубави и стойността на прага е по-висока от оценката на целевата функция. Другата е g(x), където резултатите са лоши, а прагът е по-нисък от оценката.
Правят се последващи математически изчисления, като идеята е отношението между l(x) и g(x) да се максимизира. На базата на това се избират конкретни параметри и стойностите им, които да се използват, като се взимат под внимание и предишни итерации. Това допринася за по-добри резултати с течение на итерациите.
5/ Прилагане на функцията fmin()
В основата на библиотеката Hyperopt стои функцията fmin(), чрез която се прилага Бейсовата оптимизация. Нейните основни параметри са следните:
- fn - целевата функция
- space - пространството от параметри
- trials - Trials обекта
- algo - оптимизационният алгоритъм
- max_evals - максимален брой итерации
Практически пример
За да видим на практика възможностите на Hyperopt, ще направим един пример, в който задачата е да определим дали даден клиент на банка ще се възползва от оферта за срочен депозит или не, т.е. имаме задача за бинарна класификация и двете възможни стойности за целевата променлива са да или не. Данните, които ще използваме са предварително изчистени - премахнати са ненужни колони и екстремни стойности, направен е визуален анализ и т.н.
Ако искате да научите повече за стъпките от етапа на предварителна обработка на данните, можете да прочетете в следните статии:
- Machine Learning: Как да обработим липсващи стойности при подготовката на данни за анализ?
- Machine Learning: Как да се справим с отличителни стойности (outliers)?
- Machine Learning: Защо е важно данните да са мащабирани?
- Machine Learning: Силата на визуализацията на данни. Коя графика какво ни показва?
- Machine Learning: Интерактивни визуализации с Python
- Machine Learning: Какво означава извадката да не е балансирана?
- Machine Learning: Как да кодираме категорийни променливи?
- Machine Learning: 5 начина да конструираме нови променливи
Примерът, който ще разгледаме по-надолу, можете да изтеглите от тук.
Оценка на модела без оптимизация
Ще използваме алгоритъма RandomForest при изграждане на модела за машинно обучение, като неговите параметри и техните подразбиращи се стойности можете да видите в таблицата по-долу:
| Parameter | Default value | |
|---|---|---|
| 0 | criterion | gini |
| 1 | max_depth | None |
| 2 | max_features | auto |
| 3 | min_samples_leaf | 1 |
| 4 | min samples_split | 2 |
| 5 | n_estimators | 100 |
# Създаване на модела с параметри по подразбиране
rf = RandomForestClassifier()
# Обучение на модела
rf.fit(X_train_res, y_train_res)
# Тест на модела
rf_pred = rf.predict(X_test)Резултати:
| Metrics | Values | |
|---|---|---|
| 0 | Overall Accuracy | 0.714925 |
| 1 | Overall Error | 0.285075 |
| 2 | Precision | 0.665428 |
| 3 | Specificity | 0.769231 |
| 4 | Sensitivity | 0.639286 |
| 5 | F1_score | 0.652095 |
В 71% от всички случаи класификаторът е разпределил правилно обектите в съответните класове. Определил е, че в 67% от случаите хората ще приемат офертата за депозит и те в действителност биха приели. Открил е 77% от хората, които няма да се възползват от офертата и 64% от тези, които ще приемат.
Ако искате да научите по-подробно за тези метрики, можете да прочетете в статията Machine Learning: Метрики за оценка на класификационни модели.
# Откриване на разликата между определените от класификатора класове и тези в действителност
error = df_rf['Actual'].mean() - df_rf['Predicted'].mean()41.79% в тестовата извадка са от положителния клас, а класификаторът е определил 40.14% правилно, т.е. грешката е 1.65%.
Оценка на модела след оптимизация
Първата стъпка, която трябва да предприемем при оптимизация на модела с библиотеката Hyperopt, е да създадем пространство от параметри и техните стойности.
# Създаване на речник с параметри и техни възможни стойности
params = {'criterion': hp.choice('criterion', ['entropy', 'gini']),
'max_depth': hp.quniform('max_depth', 1, 11, 1),
'max_features': hp.choice('max_features', ['sqrt','log2', None]),
'min_samples_leaf': hp.choice('min_samples_leaf', [2, 5, 10, 14]),
'min_samples_split' : hp.choice ('min_samples_split', [2, 4, 6, 8]),
'n_estimators' : hp.choice('n_estimators', [200, 500])
}За всеки от параметрите са зададени конкретни възможни стойности, които след това можем да използваме, когато създаваме модел при дефиниране на целевата функция.
# Създаване на целева функция
def objective(params):
# Създаване на модел
rf_new = RandomForestClassifier(criterion = params['criterion'],
max_depth = params['max_depth'],
max_features = params['max_features'],
min_samples_leaf = params['min_samples_leaf'],
min_samples_split = params['min_samples_split'],
n_estimators = params['n_estimators'],
)
# Изчисляване на обща точност
accuracy = cross_val_score(rf_new, X_train_res, y_train_res, cv = 5).mean()
# Полученият резултат трябва да е с отрицателен знак, защото се стремим да намерим максимум обща точност
return {'loss': -accuracy, 'status': STATUS_OK }Като метрика за оценка при целевата функция задаваме общата точност (accuracy). Тъй като целта е да се намерят тези стойности на параметрите, при които общата точност е най-висока, а при Hyperopt алгоритъмът се стреми да открие минимума на функцията, е необходимо да сменим знака на получения резултат с отрицателен.
Следващата стъпка е да използваме функцията fmin(), чрез която да открием оптималните параметри. На нея като параметри подаваме целевата функция objective, пространството от параметри params и trials обекта. Алгоритъмът за търсене задаваме да е tpe.suggest и броят итерации да бъде 80, т.е. ще се пробват 80 комбинации на параметрите и техните стойности и накрая ще получим като резултат най-добрата.
# Създаване на Trials обект
trials = Trials()
# Използване на функцията fmin()
best = fmin(fn= objective,
space= params,
algo= tpe.suggest,
max_evals = 80,
trials= trials)Резултат:
| Parameters | Values | |
|---|---|---|
| 0 | criterion | 1 |
| 1 | max_depth | 10 |
| 2 | max_features | 1 |
| 3 | min_samples_leaf | 0 |
| 4 | min_samples_split | 0 |
| 5 | n_estimators | 0 |
При тези параметри, които са зададени с hp.choice, получаваме индекс, показващ позицията на конкретната стойност в зададения списък. Необходимо е за тях да създадем отделни речници с конкретните индекси и техните съответстващи стойности.
criterion = {0: 'entropy', 1: 'gini'}
m_features = {0: 'sqrt', 1: 'log2', 2: None}
n_est = {0: 200, 1: 500}
split = {0: 2, 1: 4, 2: 6, 3: 8}
leaf = {0: 2, 1: 5, 2: 10, 3: 14}Оптималните параметри, определени от функцията fmin(), можете да видите в таблицата по-надолу:
| Parameters | Values | |
|---|---|---|
| 0 | criterion | gini |
| 1 | max_depth | 10 |
| 2 | max_features | log2 |
| 3 | min_samples_leaf | 2 |
| 4 | min_samples_split | 2 |
| 5 | n_estimators | 200 |
След като вече имаме оптималните параметри, можем да създадем новия модел.
# Създаване на модел с оптималните параметри
trainedforest = RandomForestClassifier(criterion = criterion[best['criterion']],
max_depth = best['max_depth'],
max_features = m_features[best['max_features']],
min_samples_leaf = leaf[best['min_samples_leaf']],
min_samples_split = split[best['min_samples_split']],
n_estimators = n_est[best['n_estimators']])
# Обучение на модела
trainedforest.fit(X_train_res, y_train_res)
# Тест на модела
rf_new_pred = trainedforest.predict(X_test)Основните метрики за оценка на класификационни модели са със следните стойности:
| Metrics | Values | |
|---|---|---|
| 0 | Overall Accuracy | 0.756716 |
| 1 | Overall Error | 0.243284 |
| 2 | Precision | 0.736842 |
| 3 | Specificity | 0.833333 |
| 4 | Sensitivity | 0.65 |
| 5 | F1_score | 0.690702 |
Моделът е със 76% обща точност. В 74% от случаите правилно е определил обектите от положителния клас, които в действителност са положителни. Открил е 83% от отрицателния клас и 65% от положителния.
# Откриване на разликата между определените от класификатора класове и тези в действителност
error = df_rf_best['Actual'].mean() - df_rf_best['Predicted'].mean()41.79% от обектите в тестовата извадка спадат към положителния клас, а класификаторът е определил правилно 36.86% от тях. Имаме 4.93% грешка.
Сравнение на резултатите
В следната сравнителна таблица можете да видите разликата в стойностите на различните метрики за оценка на класификационни модели за модела с параметри по подразбиране и след оптимизация.
| Metrics | RF Default | RF Best Params | |
|---|---|---|---|
| 0 | Overall Accuracy | 0.714925 | 0.756716 |
| 1 | Overall Error | 0.285075 | 0.243284 |
| 2 | Precision | 0.665428 | 0.736842 |
| 3 | Specificity | 0.769231 | 0.833333 |
| 4 | Sensitivity | 0.639286 | 0.65 |
| 5 | F1_score | 0.652095 | 0.690702 |
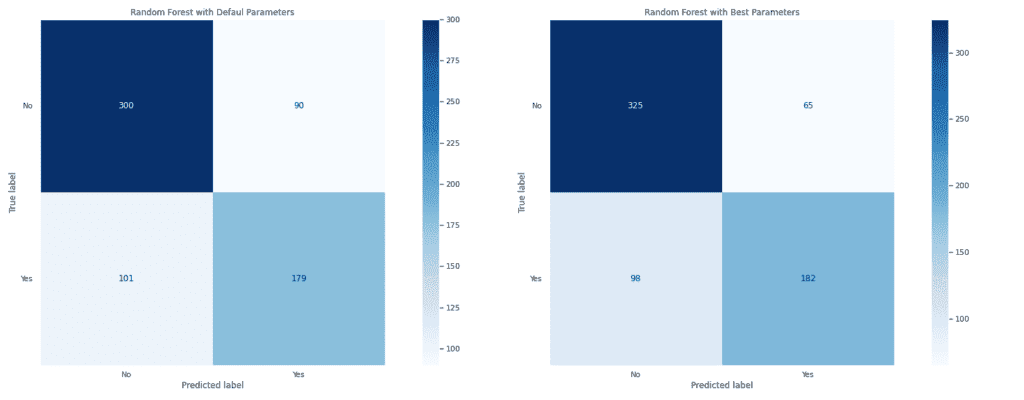
Наблюдава се подобрение във всичките метрики след извършване на оптимизация. Това може да се види и в графиките на матрицата на неточностите и на ROC и Precision-Recall кривите.
Моделът с оптимални параметри има по-добри резултати, защото стойностите на False Positive и False Negative са по-ниски от тези, изобразени на матрицата на модела с параметри по подразбиране. Правилно е определил 325 от общо 390 обекта от отрицателния клас и 182 от 280 от положителния клас.
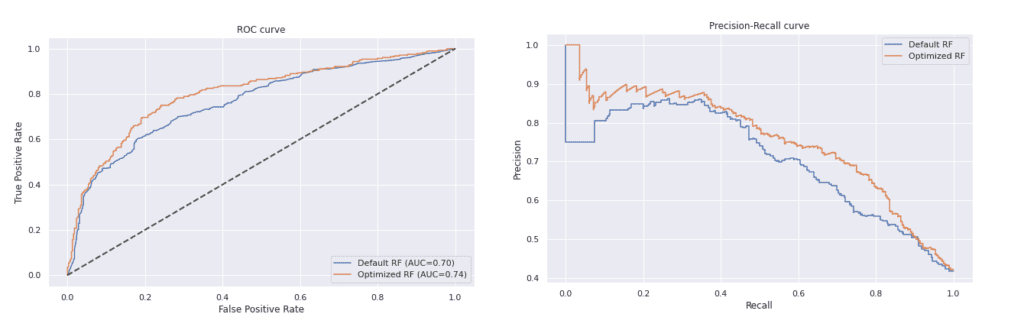
Съдейки по двете графики, оптимизираният модел дава по-добри резултати от този с параметри по подразбиране. Неговата ROC крива е с по-голяма площ под кривата и е по-далеч от нулевия класификатор, а Precision-Recall кривата му е по-близко до горния десен ъгъл на графиката отколкото тази на другия модел.
Извод
Библиотеката Hyperopt предоставя много възможности за оптимизация на модел за машинно обучение, най-вече при задаване на пространството от параметри и техните стойности. При нея предимство е това, че взима под внимание предишни итерации при търсене на най-добрите стойности за параметрите, което ѝ позволява по-бързо да открие тези, които са оптимални.
Искате да научите повече за машинното обучение?
Включете се в курса по машинно обучение и анализ на данни с Python.
Автор: Десислава Христова